РАЙ МАТЕМАТИЧЕСКИХ HАУК. ЧАСТЬ ПЕРВАЯ

“Механика — рай математических наук, посредством нее достигают математического плода”.

Е, 8 об., стр.84.

“Пусть не читает меня тот, кто не математик”,— заявлял Леонардо (W. An. IV, 14 об., стр. 12). Математические науки (арифметика и геометрия) обладают, по его словам, высшей достоверностью, накладывают “молчание на языки спорщиков”, приводят “к вечному молчанию” всякое возражение, прекращают ненавистный Леонардо крик (Т. Р., 33, стр. 9—10).

“Тот, кто порочит высшую достоверность математики, тот питается сумбуром и никогда не заставит умолкнуть противоречия софистических наук, которые учат вечному крику...” (W. An. II, 14, стр. 20).

Сопоставим эти слова с афоризмом, взятым в качестве эпиграфа: “Механика — рай математических наук, посредством нее достигают математического плода”.

Кажется, все ясно. Математика и механика провозглашены двумя верховными науками — Леонардо не только “предтеча” механико-математического миросозерцания, но и первый его представитель. На самом деле вопрос сложнее, чем это кажется.

Прежде всего, когда Леонардо говорил о механике, он понимал под этим словом не теоретическую дисциплину, а практическое применение теоретических положений. Именно потому он и говорил, что посредством механики “достигают математического плода”. Книгам, которые Леонардо проектировал, он давал заглавие не “Механика”, а “Элементы машин” или, точнее, “Начала построения машин” (Elementi rnacchinali) — по образцу “Начал” Евклида (А, 10, стр. 84); он также упоминал “Книгу о науке машин” (libro della scientia delle machine, W. An. I, 13 об., стр. 84).

Точно так же и Лука Пачоли говорил не о леопардовой книге по механике, а о “неоцененном произведении, посвященном пространственному движению, удару, тяжестям и всяческим силам, т. е. акцидентальным тяжестям”,—произведении, которое Леонардо готовился завершить в конце 90-х годов.

Наконец, Леонардо прямо противопоставлял “механическое доказательство” (prova meccanica) “механике”. “Доказательство это тем более достойно похвалы, — говорил он, — чем более непосредственно, само собою, дает ту же самую истину, какую дает и механика” (С. А., 231а, стр. 84—85). Совершенно очевидно, что слово “механика” здесь употреблено в значении “механического искусства”. Благодаря “механике” реализуются теоретические положения “математики”, которая включает и то, что мы теперь называем теоретической механикой.

Что “математика” охватывала у Леонардо не только чисто математические дисциплины, но и физику, явствует из его восклицания: “О математики, пролейте свет на это заблуждение! Дух не имеет голоса, ибо где голос, там тело. ..” и т. д. (см. ИП, стр. 19). Очевидно, что не математики, а физики (в современном значении слова) занимаются вопросами акустики, а потому и призваны опровергать разглагольствования о “голосах духов”. Когда Леонардо утверждал, что “птица — действующий по математическому закону и инструмент” (С. А., 161а, стр. 596), он опять-таки явно имел в виду не математику, а то, что теперь называется механикой.

Может показаться, что от такого переименования механики (или физико-математических наук в целом) в математику существо дела не меняется. Идеал математико-механического описания и объяснения природы как будто остается в обоих случаях тем же. На самом деле это не так.

Требование “пусть не читает меня тот, кто не математик” ведь уже не относится тогда к чистой математике или к математике в строгом значении слова. Иной смысл получает и другой афоризм Леонардо: “Никакой достоверности нет в науках там, где нельзя приложить ни одной из математических наук, и в том, что не имеет связи с математикой” (G, 96 об., стр. 12). Это вовсе не то же самое, что заявление Канта: “Я утверждаю, что в каждой специальной естественной науке можно найти собственно науки лишь столько, сколько в ней математики”. У Леонардо речь идет о физико-математических науках, у Канта — о математике как таковой.

Чтобы окончательно убедиться в этом, попробуем пересмотреть еще раз приведенные и некоторые другие высказывания Леонардо да Винчи уже не так, как они даются обычно в антологиях, вне контекста, а в связи с тем конкретным поводом, который побудил к ним. “Пусть не читает меня тот, кто не математик”,— было сказано при описании механизма сердечных клапанов. “Тот, кто порочит высшую достоверность математики”, — было сказано опять в связи с рисунком сердца. “А потому, о изучающие, изучайте математику и не стройте без фундаментов”,— после длинного рассуждения о движениях при дыхании и пищеварении (W. An. IV, 14 об.). “Все это я опишу и нарисую подробно, доказывая эти движения на основе моих математических начал”, — о движении мускулов рта (W. An. В, 29).

Но тогда встает новый вопрос: что же представляло собою то математизированное естествознание, та “математика”, которую Леонардо считал нужным положить в основу всех наших знаний? Для ответа на этот вопрос обратимся к одному сопоставлению.

Друг Леонардо да Винчи, платоник и монах Лука Пачоли, также заявлял, что “из всех истинных наук, как утверждают Аристотель и Аверроэс, наши математические науки наиболее истинны и имеют первую степень достоверности, и им следуют все другие естественные науки”.

Действительно, Аристотель устанавливал градацию наук по их точности: чем проще рассматриваемое свойство, тем большей точностью обладает изучающая его наука. Геометрия, отвлекающаяся от понятия движения, точнее, чем механика; общее учение о бытии (онтология, метафизика), отвлекающееся от понятия величины, точнее, чем геометрия. Иначе говоря, чем положение отвлеченнее, тем оно точнее и достовернее. Мог ли разделить эту точку зрения Леонардо?

В “Сумме” Луки Пачоли имеется ряд задач о путешествиях, в том числе и следующая: путешественник совершил путешествий столько, сколько у него вначале было дукатов; при каждом путешествии он удваивал число их и в конце концов имел 90 дукатов; спрашивается, сколько путешествий он совершил?

В отличие от Пачоли Леонардо всегда интересовался физическим смыслом того или иного алгоритма, диапазоном его возможного применения к фактам физического мира. Определив соотношение между величиной крыла и весом летучей мыши, Леонардо предостерегал от поспешного заключения, что то же самое соотношение должно сохраняться всюду и всегда, т. е. при постепенном увеличении веса у других животных. “Я говорю, что если летучая мышь весит 2 унции и простирает крыло на 1/2 локтя, то орел, соразмерно с этим, должен был бы простирать крыло на 60 локтей, не меньше. Между тем мы видим на опыте, что орел не превосходит ширину 3 локтей. И многим, не видевшим никогда этих животных, показалось бы, что одно из них не может летать; они сочли бы, что если у летучей мыши ее вес хорошо спропорционирован с шириной ее крыльев, то у орла эта ширина недостаточна; а если орел хорошо держится на своих крыльях, то летучая мышь имеет слишком большие крылья, несоразмерные и бесполезные для нее. Мы видим, однако, что и летучая мышь и орел держатся на своих крыльях с величайшей ловкостью, а в особенности летучая мышь, которая своими быстрыми поворотами и изворотами может одолеть стремительные налеты и ускользнуть от мошек, мух и тому подобных мелких животных” (В, 89 об., стр. 600—601).

Другой пример. Леонардо возражал Альберту Саксонскому, указывая, что перипатетическая формула v = k p/m

(где v — скорость, р — сила, т — вес тела, k — коэффициент пропорциональности) не имеет универсального значения.

“О движении. Альберт Саксонский говорит в своем сочинении „О пропорциях", что если сила движет движимое с определенной скоростью, то половину его она будет двигать с двойной скоростью, что мне кажется не так...” (I, 120 об., стр. 225). Возвращаясь несколько дальше к той же теме, Леонардо писал: “И если некоторые говорили, что чем меньше приводимое в движение тело, тем более его гонит движущее, постоянно увеличивая скорость движения пропорционально уменьшению его до бесконечности, то отсюда следовало бы, что атом оказался бы едва ли не более быстрым, чем воображение или глаз, который мгновенно достигает звездной высоты”. Леонардо производит подсчеты и заключает: “Теперь смотри: если взять вес одного зернышка пыли для опыта, то бомбарда выбросила бы его не дальше, чем дым в начале выстрела, а по приведенному рассуждению она угнала бы его на миллион миль за то же самое время, за которое 100-фунтовое ядро прошло 3 мили”. Отсюда мораль: “Не доверяйте же, исследователи, тем авторам, которые одним воображением хотели посредствовать между природой и людьми; верьте лишь тем, кто, основываясь на указаниях природы и на действиях своих опытов, приучил ум свой понимать, как опыты обманывают тех, кто не постиг их природы, ибо опыты, часто казавшиеся тождественными, весьма часто оказывались различными, — как здесь это и доказывается” (I, 102 об., стр. 225—226).

Здесь выражено самое главное, что было характерным для Леонардо: не отвлеченный математический алгоритм, а закономерность, открываемая на основе “указаний природы” и “действий опытов”. Дж. де Сантильяна совершенно прав, утверждая, что математика у Леонардо — не “созерцание сверхчувственного мира, а поиски геометрического костяка реальности”.

Разумеется, и Пачоли не разрывал всякую связь математики с практикой и техникой. Наоборот, он всячески подчеркивал значение математики для фортификации, артиллерии, архитектуры, гидротехники, картографии, теории перспективы, музыки и т. д. Он говорил, что “золото испытывается огнем, а дарование математикой”. Но он же приводил надпись Платона над входом в Академию: пусть не входит сюда тот, кто не знает геометрии, и высшее достоинство математики усматривал в ее “величайшей абстрактности и тонкости — grandissima abstractione e subtigliezza”, в том, что она отвлекается от “чувственной материи”.

Во времена Леонардо и Пачоли существовала и третья точка зрения на природу и значение математики. Она была представлена флорентийскими платониками типа Фичино и их единомышленниками, к числу которых принадлежал Джованни Пико делла Мирандола. Пять тезисов этого последнего заслужили безоговорочное одобрение Фичино. В этих тезисах заявлялось, что “математика не есть настоящее знание”, что она “не ведет к блаженству”, что математические науки “не существуют ради них самих”, что “нет ничего более вредного для теолога, чем частые и усидчивые занятия математикой Евклида”. Этого рода мистическому платонизму был чужд не только Леонардо, но и ссылавшийся на Платона Лука Пачоли.

Среди математических фрагментов Леонардо да Винчи одно из первых мест занимает большой кусок из кодекса Форстера I, представляющий собою в известном смысле законченное целое. Он обозначен самим Леонардо, как “Книга, озаглавленная О преобразовании, т. е. о преобразовании одного тела в другое без убавления пли возрастания материи”. Практическая направленность трактата становится совершенно очевидной из начальных его строк: “Геометрия, охватывающая преобразования металлических тел, которые состоят из вещества, способного растягиваться и сокращаться в зависимости от того, что необходимо изучающим их”. Это — самое систематическое из произведений Леонардо, разделенное на книги (или разделы) и нумерованные положения. Оно посвящено преобразованию площадей в равновеликие площади и тел в тела, равновеликие по объему. Уже из приведенных строк Леонардо явствует, что именно с этими задачами ему приходилось встречаться при обработке металла — чеканке, отливке деталей, при работе в качестве скульптора (в частности, при проектировании конной статуи Сфорца), при строительных и гидротехнических расчетах и т. д. Даже говоря о геометрии, Леонардо не терял из виду “металлических тел”. Дело не в узком прикладничестве. Дело в том, что “математические науки”, “математика” были для Леонардо “опытными дисциплинами”.

Не случайно Леонардо да Винчи был изобретателем многочисленных приборов, предназначенных для решения математических задач: пропорциональный циркуль, прибор для решения так называемой Алхазеновой задачи (найти точку отражения на сферическом выпуклом зеркале по данным точкам глаза и предмета), прибор для вычерчивания параболы, прибор для построения параболических зеркал.

По Леонардо, “наука о тяжестях вводима в заблуждение своею практикою”. Почему? потому, что оси весов, “по мнению древних философов, имеют природу математической линии, и в некоторых случаях являются математическими точками, — точками и линиями, которые бестелесны; практика же полагает их телесными, потому что так велит необходимость, раз они должны поддерживать тяжесть этих весов вместе с взвешиваемыми на них грузами”.

Ошибки “древних”, по Леонардо, проистекали из того, что они смешивали выводы, основанные на исследовании чисто математического, абстрактного рычага и рычага весомого, физического (С. А., 93 об. b, стр. 127-128).

Самого Леонардо прежде всего интересовал именно весомый рычаг, а “бестелесный” математический рычаг мог представлять для него лишь вторичный интерес, как вспомогательное средство для перехода к более конкретному. Этим объясняются такие леонардовские памятки: “Проверь на опыте и опиши природу осей весов, когда они толсты или тонки, находятся в середине, внизу или наверху или занимают промежуточное положение между указанными” (С. А., 146с, стр. 128).

Можно было бы напомнить в той же связи леонардовское противопоставление “математической” и “натуральной” или “механической” точки (С. А., 200Ь): “Между механической точкой и точкой математической разница бесконечная, ибо механическая — видима, а следовательно, имеет непрерывную величину, а все непрерывное делимо до бесконечности; математическая же точка невидима и не имеет никакой величины; а там, где нет величины, там нет деления”.

Идет ли речь о спрямлении дуги окружности, Леонардо обращается к образу вращающегося колеса: “Движение повозок всегда показывало нам, как спрямлять окружности круга” (Е, 25 об., стр. 75—76). Или еще определеннее: “Животные, движущие повозки, дают нам очень простое доказательство квадратуры круга, доставляемое колесами этих повозок, посредством следов обода, образующего прямую линию” (G, 58).

Правда, в других местах Леонардо критиковал подобный подход и намекал на возможность более строгого и точного. “Витрувий измерял мили посредством многих полных оборотов колес, движущих повозки, разворачивая на много стадий линии окружностей этих колес. Однако он этому научился от животных, движущих такие повозки, и не знал способа построить квадрат, равный кругу. Этот способ первым нашел Архимед Сиракузский а именно: умножение радиуса круга на половину окружности дает прямоугольник, равный кругу” (G, 96). В другом месте Леонардо пытался дополнить Архимеда, упоминая об изобретенном им приеме, который основал на пренебрежении ничтожно малой величиной: “Архимед дал квадратуру многоугольника, а не круга. Следовательно, он никогда не квадрировал фигуры с криволинейными сторонами. А я квадрирую круг минус доля столь малая, какую может вообразить интеллект, то есть как видимая точка” (W. 12280 = R. 1475).

Иными словами, Леонардо довольствовался чаще всего приближенными решениями, достаточными для инженера, но не удовлетворяющими требованиям математической строгости. Таков был, например, его подход к построению описанного круга при заданной длине стороны многоугольника (В, 14).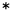

По Леонардо, “пропорция обретается не только в числах и мерах, но также в звуках, тяжестях, временах и положениях и в любой силе, какая бы она ни была” (К, 49, стр. 12). Отсюда обилие афоризмов и заметок, построенных по схеме: tanto—quanto, насколько—настолько (или: во столько раз—во сколько). Это “чем больше — тем больше”, или “чем меньше — тем меньше” в самой общей форме чаще всего простейшая линейная зависимость, имеющая в виду простейшие действия с величинами первой степени по тройному правилу. Отсюда — примитивизация, упрощение проблемы. Так, например, сила света убывает пропорционально первой степени расстояния (С, 22, стр. 649—650); такая же линейная зависимость Между интенсивностью Цвета, расстоянием и плотностью воздуха.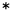

Точно так же зависимость степени освещенности от угла падения световых лучей определялась Леонардо либо в самой общей и неопределенной форме, либо в форме простейшей пропорциональности, тогда как на самом деле степень освещенности пропорциональна косинусу угла, образуемого лучами с нормалью к освещенной части поверхности.

Определяя нормальные (канонические) пропорции человеческой фигуры, Леонардо обычно указывал сравнительно простые отношения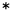. Впрочем, ошибочно думать, что это должно было непременно означать схематизацию и неуклонное оперирование “жесткими” целочисленными соотношениями, игнорирующими всяческие нюансы. Господство простейших целочисленных “музыкальных” отношений в теоретических трактатах Возрождения, от Альберти до Виньолы, вовсе не исключало более сложных иррациональных отношений, наоборот, предполагало их как свою основу. “Музыкальные” отношения служили лишь средством более просто и доходчиво, но вместе с тем лишь приближенно (и всегда приближенно) определять иррациональные соотношения, почти неизбежно появляющиеся при любых геометрических построениях (диагональ квадрата и т. п.).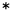

Чрезвычайно показательно в этом отношении рассуждение Луки Пачоли. Разбирая указание Витрувия относительно того, что колонны второго яруса портиков, окружающих форум, должны делаться на одну четверть ниже, чем колонны первого яруса, в подражание “природе растений, например, таких стройных деревьев, как ель, кипарис и сосна”, Пачоли писал своим тяжеловесным, неуклюжим стилем: “... нижние колонны должны быть в зданиях подножием, корнем и основанием для всего, расположенного над ними, наподобие древесного ствола, служащего поддержкой для всех прочих ветвей, находящихся над ними, каковые всегда бывают более слабыми, чем подножие. Однако точная величина нам неизвестна в своем определенном выражении. Поскольку же искусство подражает природе в меру всех своих сил и Витрувий не взял в точности должное отношение ветвей и вершин к их стволам или массивам и подножиям, ведь оно нам никогда не может стать известно, разве только всевышний сподобит нас этого, как говорит Платон в своем „Тимее", ... постольку, дабы искусство Не двигалось ощупью, но всегда с наибольшей возможной для него уверенностью, Витрувий указывает отношение, для нас известное и определенное, которое рационально и всегда может быть выражено числом, говоря, что колонны вверху следует делать на четверть меньше, чем колонны нижние”. Эти слова Пачоли проливают свет на загадочное соотношение между первой частью его трактата, где речь идет об иррациональном "золотом сечении", и третьей частью, где все архитектурные пропорции — целочисленные. Отношения целых чисел — лишь приближения к сложнейшим отношениям самой природы, доказуемым геометрически, но невыразимым арифметически с абсолютной точностью.

Но даже если допустить, что целый ряд числовых отношений у Леонардо соответствует приближенным и округленным значениям, нельзя не видеть, что математический аппарат и математические формулировки у Леонардо да Винчи почти всегда просты — неизмеримо проще, чем те широкие и сложные задачи, которые он ставил и которые не могли быть с исчерпывающей полнотой решены средствами старого математического аппарата. Это была отнюдь не только личная трагедия Леонардо, которую можно было бы объяснить характером полученного им математического образования. Математика времен Леонардо принадлежала тому периоду, когда переменная величина еще не стала кардинальным понятием этой науки, а потому математика этого времени еще не могла овладеть сложными проблемами движения, которые настойчиво ставило перед учеными развивающееся естествознание.

Особенно наглядно указанное несоответствие проступает в гидродинамике. Первый труд по гидродинамике появился лишь в 1638 г. — труд ученика Галплея, Бенедетто Кастелли “Delia misura dell´acque correnti” (“О мере движущихся вод”). “Гидродинамика” Даниила Бернулли появилась ровно сто лет спустя, в 1738 г., когда стало возможным применить в этой области новый математический аппарат, позволявший овладеть проблемами движения. Уделом Леонардо должны были остаться наблюдение и эксперимент. При чтении многих описаний движения воды перед читателем прежде всего встает облик Леонардо, зорко наблюдающего особенности течения рек, вглядывающегося в особенности берегов, подобных камней и т. д. Здесь — опыт гидротехника, опыт корабельщика, опыт пловца.

“Если хочешь правильно судить о всех фигурах движений и течений воды, смотри на светлую воду малой глубины под лучами солнца, и тогда ты увидишь, благодаря солнцу, все тени и все светлые места этих движений и предметов, уносимых водой” (F, 65 об., стр. 362).

“Естественно обнажившееся дно реки не дает настоящих указаний о природе предметов, уносимых водой, и о их количестве, ибо в глубоких водах многие места покрыты песком, а при понижении уровня отдельные боковые течения реки уносят затем этот песок с гальки, на которой он лежал, и обнажают ее. При этом постепенно разрушаются высокие валы этого песка, и он, благодаря своей легкости, уносится течением реки, а затем отлагается ею там, где течение воды более спокойно” (L, 32, стр. 362).

Неслучайно, что некоторые наблюдения над движущейся водой точно локализованы. Леонардо говорит о реке По и о размыве ее берегов (А, 23 об., стр. 365), о лестнице в Виджевано под замком Сфорца с 130 ступеньками, по которой низвергается вода (Leic., 32, стр. 345), или делает краткую заметку: “Морские волны у Пьомбино. Вся вода пенится” (W. 12665, стр. 354).

Несоответствие между простотой математического аппарата и сложностью задач, которые Леонардо пытался решать в физике и технике и среди которых проблема движения занимала первое место, сделало естественным стремление заменять в ряде случаев математический вывод непосредственной опытной констатацией искомых количественных соотношений между явлениями, т. е. заменять вычисление измерением. Не случайным является значительное число измерительных приборов в заметках Леонардо, как им самим изобретенных, так и известных уже раньше. Таковы прибор для измерения скорости ветра, приборы для измерения пути (со ссылками на Витрувия и Леона-Баттиста Альберти) или гигрометр, известный уже ранее Николаю Кузанскому и тому же Альберти.

Леонардо проявляя известный интерес к алгебре, Среди его записей можно найти такие заметки для памяти: “Альберт из Имолы, „Алгебра", т. е. показание того, как число и неизвестное (cosa) приравниваются к [другому?] неизвестному числу (cosa numero)” (К, 75 об., стр. 26). Или: “Алгебра, которая находится в семье Марлиани и написана их отцом” (С. А., 225Ь, стр. 26). Но Леонардо да Винчи не мог бы никоим образом внести в свои записные книжки заявление, подобное тому, которое 300 лет спустя сделал Лагранж в предисловии к “Аналитической механике” (1788): “В этой работе совершенно отсутствуют какие бы то ни было чертежи. Излагаемые мною методы не требуют ни построений, ни геометрических или механических рассуждений; они требуют только алгебраических операций, подчиненных планомерному и однообразному ходу. Все любящие анализ с удовольствием убедятся в том, что механика становится его новой отраслью, и будут мне благодарны за то, что этим путем я расширил область его применения”.

У Леонардо как раз наоборот: его рассуждения требуют чертежей, непонятны без геометрически наглядных образов. Его рассуждения всегда геометрические или геометрико-механические.

Под углом зрения механики рассматривал Леонардо да Винчи и функции живых организмов. Как художник и скульптор, он уделил значительное внимание объяснению поз и положений человека общими законами механики. Так, например, разъясняя два вида “равновесия или балансирования люден”, Леонардо переходил к совету, как изображать борьбу Геркулеса с Антеем. “Изображая Геркулеса, который стискивает Антея, приподняв его над землей, между своею грудью и руками, делай его фигуру настолько позади центральной линии его ступ ней, насколько у Антея центр тяжести находится вперед тех же ступней” (Т. Р., 394, стр. 847). Движение чело века, тянущего груз, бегущего, поднимающегося и спускающегося по лестнице, не только фиксируется в рисунках и описаниях, но и анализируется с точки зрения общих механических законов. Леонардо внимательно изучал механизм поворачивания руки ладонью вверх и ладонью вниз (W. An. I, 1 об.) и т. д. и т. д. Анализируя движения, он как бы насквозь видел человеческое тело, связывая эти движения со строением костей и скелета. В рисунках Леонардо скелет всегда воспринимается на фоне возможных его движений. По выражению одного из исследователей (Холля), скелеты Леонардо “живут”.